We have seen in chapter
1 that an x-ray beam is an electromagnetic wave characterized by an electric
field whose strength varies sinusoidally with time at any one point in the
beam. Since an electric field exerts a force on
a charged particle such as an electron, the oscillating electric field
of an x-ray beam will set any electron it encounters into oscillatory motion
about its mean position.
Now an accelerating or
decelerating electron emits an electromagnetic wave. We have already seen an
example of this phenomenon in the x-ray tube, where x-ray are emitted because
of the rapid deceleration of the electrons striking the target. Similarly, an
electron which has been set into oscillation by an x-ray beam is continuously
accelerating and decelerating during its motion and therefore emits an electromagnetic wave. In this sense,
an electron is said to scatter x-rays, the scattered beam being simply the beam
radiated by the electron under the action of the incident beam. The scattered
beam has the same wavelength and frequency as the incident beam and is said to
be coherent with it, since there is a definite relationship between the phase
of the scattered beam and that of the incident beam which produced it. (the
phase change on scattering from an electron is λ/2. Because it is exactly the
same for all the electrons in a crystal, it cancels out in any consideration of
phase differences between rays scattered by different atoms, as in fig. 3-2,
and so does not affect the derivation of the Bragg law given in Sec. 3-2).
Although x-ray are
scattered in all directions by an electron, the intensity of the scattered beam
depends on the angle of scattering, in a way which was first worked out by J.
J. Thomson. He found that the intensity I
of the beam scattered by a single electro of charge e coulombs (C) and mass m kg,
at a distance r meters from the
electron, is given by
Where Io = intensity of the
incident beam, μo= 4π x 10-7 m.kg.C-1, K=
constant, and α= angle between the scattering direction and the direction of
acceleration of the electron.
Fig.
4-3
Suppose the incident
beam is travelling in the direction Ox (Fig. 4-3) and encounters an
electron at O. we wish to know the
scattered intensity at P in the xz plane where OP is inclined at a scattering
angle of 2θ to the incident beam. An unpolarized incident beam, such as that
issuing from an x-ray tube, has its electric vector E in a random direction in
the yz plane. Ths beam may be resolved into two plane-polarized components,
having electric vectors Ey and Ez where
Page 109-111
The
y component of the incident beam accelerate; the electron in the direction Oy.
It therefore gives rise to a scattered beam whose intensity at P is found from
Eq. (4-1) to be
Since
α = ΔyOP = π/2. Similarly, the intensity of the scattered z component is given
by
Since
α = π/2 - 2θ. The total scattered intensity at P is obtained by summing the
intensities of these two scattered components:
This
is the Thomson equation for the scattering of an x-ray beam by a single
electron. The intensity of the scattered beam is only a minute fraction of the
intensity of the incident beam; the value of K is 7,94 x 10-30 m2,
so that Ip/Io is only 7,94 x 10-26 in the
forward direction at 1 cm from the electron. The equation also shows that the
scattered intensity decreases as the inverse square of the distance from the
scattering electron, as one would expect, and that the scattered beam is
stronger in forward or backward directions than in a direction at right angles
to the incident beam.
The
Thomson equation gives the absolute intensity (in ergs/sq cm/sec) of the scattered
beam in terms of the absolute intensity of the incident beam. These absolute
intensities are both difficult to measure and difficult to calculate, so it is
fortunate that relative values are sufficient for our purposes in practically
all diffraction problems. In most cases, all factors in Eq. (4-2) except the
last are constant during the experiment and can be omitted. This last factor,
1/2 (1+cos22θ), is called the polarization factor; this is a rather
unfortunate term because, as we have just seen, this factor enters the equation
simply because the incident beam is unpolarized. The polarization factor is
common to all intensity calculations, and we will use it later in our equation
for the intensity of a beam diffracted by a crystalline powder.
There
is another and quite different way in which an electron can scatter x-rays, and
that is manifested in the Compton effect.
This effect, discovered by A. H. Compton in 1923, occurs whenever x-rays
encounter loosely bound or free electrons and can be understood only by
considering the incident beam not as a wave motion, but as a stream of x-ray
quanta or photons, each of energy hv1. When such a photon strikes a
loosely bound electron, the collision is an elastic one like that of two
billiard balls (Fig. 4-4). The electron is knocked aside and the photon is
deviated through an angle 2θ. Since some of the energy of the incident photon
is used in providing kinetic energy for the electron, the energy hv2
of the photon after impact is less than its energy hv1 before
impact. The wavelength λ2 of the scattered radiation is thus
slightly greater than the wavelength λ1 of the incident beam, the
magnitude of the change being given by the equation
The
increase in wavelength depends only on the scattering angle, and it varies from
zero in the forward direction (2θ = 0) to 0.05 Ǻ in the extreme backward
direction (2θ = 180⁰).
Radiation
so scattered is called Compton modified
radiation, and, besides having its wavelength increased, it has the
important characteristic that its phase
has no fixed relation to the phase of the incident beam. For this reason it
is also known as incoherent radiation. It cannot take part in diffraction
because its phase is only randomly related to that of the incident beam and
cannot therefore produce any interference effects. Compton modified scattering
cannot be prevented, however, and it has the undesirable effect of darkening
the background of diffraction patterns.
(it
should be noted that the quantum theory can account for both the coherent and
the incoherent scattering, where as the wave theory is applicable only to the
former. In terms of the quantum theory, coherent scattering occurs when an
incident photon bounces off an electron which is so tightly bound that the
electron receives no momentum from the impact. The scattered photon therefore
has the same energy, and hence wavelength, as it had before).







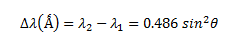
Post a Comment